Segment Trees
Segment trees are a good avenue for exploration because they allow us to quickly do updates, along with quickly finding properties for a range of our search space. However, it turns out that they are not a good approach for our Karnaugh Map simplifier, as illustrated below.
First, it's important to take note of what is a segment tree. Segment trees are a data-structure that allow us to do range queries, while working with updates. They provide similar performance to binary indexed trees / fenwick trees, but they are more useful because we can do it on more properties. Though they have been papers published on doing RMQ (range minimum query) and other operations on BIT, they are more commonly performed on segment trees.
Understanding 1D Interpretation
While a full explanation of segment trees is beyond the scope of this page, the main idea behind them is to pre-process the dataset in the form of a binary tree, and each node as you go down the binary will represent the answer within a range that gets divided into two components each time.
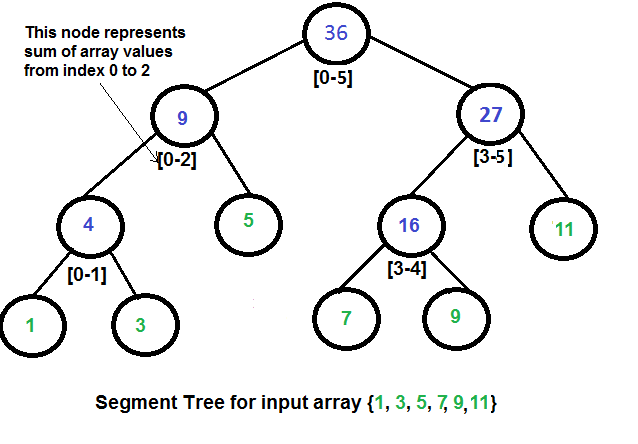
Consider the following segment tree designed for subarray sum, taken from GeeksForGeeks. We notice that the leafs are values from the original array, and the represent segments. The advantage is that if we want to query for any segment, we can do so in O(logn) time! We can also constructor the tree in O(n) time.
Extending Interpretation to 2D
Moving segment trees to 2D can take two approaches. The first approach is that we generate an array of segment trees bounded by an axis, such that when you do a query you repeat it against each segment tree on that row. For instance, if you have an NxM grid, you will have N values along the x axis and M values for y. To perform a query, we will iterate along the x axis, thus each query takes O(n*log(y)) time. The other, better approach would do to make two sets of segment trees which with some tricky processing you can achieve O(log(x) * log(y)) time. Any further explanation is beyond the scope of this documentation.
What do we achieve?
We can use a similar algorithm as the 2D prefix sum approach from before, except we do not need to recompute the 2D prefix sum array entirely, and instead we can just update the binary trees. However, this quickly becomes a not-so-good solution when we notice that the actual query operations take significantly more time than updating. Hence, this solution becomes strictly inferior to the solution we had prior, because before we took range sum in O(1) time versus O((logM) * (logN)) time using 2D segment trees.
To conclude, 2D segment trees are not a good approach for this problem.